Mixture of Inputs Summary

Text Generation Beyond Discrete Token Sampling

• 2025-05; Zhuang, Liu, Singh, Shang, Gao

High-Level Ideas

• Training-free method that enables human-like 'fluid' reasoning before being articulated as natural language

• Standard Chain-of-Thought (CoT) sample one token per step and follow that path, potentially abandoning valuable alternatives

• Mixture of Inputs feeds both the sampled token and its probability distribution

• A Bayesian method is used: the token distribution is the prior and the sampled token the observation*

• It's related to superposition of all possible tokens: it's a convex combination, weighted by probabilities

• This flexibility enables the exploration of different reasoning paths, and avoids making hard (consequential) decisions too early

*It's not clear to me how updating a prior from a draw from itself is helpful: how is the observation evidence of anything? See below for elaboration

Related Papers

• Soft Thinking: Unlocking the Reasoning Potential of LLMs in Continuous Concept Space

• Reasoning by Superposition: A Theoretical Perspective on Chain of Continuous Thought

Some Discussion

The underlying ideas are similar to soft thinking, but a little more refined. In vanilla Chain-of-Thought (CoT) prompting, the sampled intermediate reasoning token is fed back into the prompt. This is a one-hot encoding, and discards the information from the distribution; if a rare token is sampled, the bulk is forgotten. In essence, a single path is taken. Mixture of Inputs (MoI) feeds a distribution back into the LLM, namely, a mixture of the (one-hot encoded) sampled token and the underlying probability distribution. (Soft thinking uses only the distribution, and is called Direct Mixture here.)

The particular mixture is chosen through Bayesian inference: the distribution of the sampled token is the prior, and the sampled token the observation. No theoretical justification is given—unlike the approximations for soft thinking. Roughly, it feels to me that soft thinking is a bit too 'vague', trying to handle all (exponentially many) paths. MoI tries "[to balance] the concrete and the probabilistic aspects of cognition" by including the sampled token.

Some Details

Let $e_i \in \mathbb R$ denote the embedding of token $i \in V$. MoI feeds a mixture (convex combination)

$$\textstyle h_t = \sum_{i \in V} w_{t, i} e_i \quad\textsf{where}\quad w_{t,i} \ge 0 \text{ and } \sum_{i \in V} w_{t, i} = 1.$$

Soft Thinking/Direct Mixture takes $w_{t, i} = p_{t, i}$, where $p_t = (p_{t,i})_{i \in V}$ is the next-token distribution at step $t$. Mixture of Inputs mixes this with the observed token. Let $y_{t,i} \in \{0, 1\}$ be the indicator that token $i \in V$ is chosen. Let

$$w_t \sim \textup{Dir}(\alpha_t) \quad\text{and}\quad y \sim \textup{Multinomial}(w_t)$$

where $\alpha_t = H(p_t) p_t$ and $H(p_t)$ is the normalised entropy:

$$\textstyle H(p) = - (\log |V|)^{-1} \sum_{i \in V} p_i \log p_i \in [0, 1].$$

Recall that the Dirichlet distribution $\textup{Dir}(\alpha)$ is a continuous, multivariate probability distribution with pdf

$$\textstyle f_\alpha(x) \propto \prod_i x_i^{\alpha_i - 1} \quad\text{for $x$ in the simple—ie, $x_i \ge 0$ and $\sum_i x_i = 1$.}$$

If $\alpha = H(p) p$, then the total concentration $\alpha_0 := \sum_{i \in V} \alpha_i = H(p)$ increases as the uncertainty (of $p_t$) increases. Whilst the expectation $\mathbb E[w_i] = \alpha_i / \alpha_0 = p_i$ doesn't depend on the (normalised) entropy $H(p)$, the variance does, but only weakly:

$$\mathbb V\textup{ar}[w_i] = p_i (1 - p_i) / \bigl(1 + H(p)\bigr) \in \bigl[ \tfrac12 p_i (1 - p_i), p_i (1 - p_i) \bigr].$$

Instead of this exact formulation an estimation is used, with a concentration hyperparameter $\beta \ge 0$:

$$w_{t, i} := \tfrac1{\beta + 1} \bigl( H p_{t, i} + (\beta + 1 - H) y_{t, i} \bigr).$$

This can be formulated as

$$w_{t, i} = \tfrac1{\beta + 1} \bigl( H p_{t,i} + (1 - H) y_{t,i} + \beta y_{t,i} \bigr) \to \begin{cases} p_{t,i} & \text{as } H \to 1 \text{ and } \beta \to 0, \\ y_{t,i} & \text{as } H \to 0 \text{ or } \beta \to \infty, \end{cases}$$

providing an interpolation between just the distribution (Direct Mixture/Soft Thinking) and just the token (CoT). The connection with the Dirichlet prior isn't so clear to me.

Results

In summary, I'd suggest the results are good, but far from outstanding: the average improvement is under 2pp (absolute) and 3% (relative), giving each model–benchmark pair equal weight.

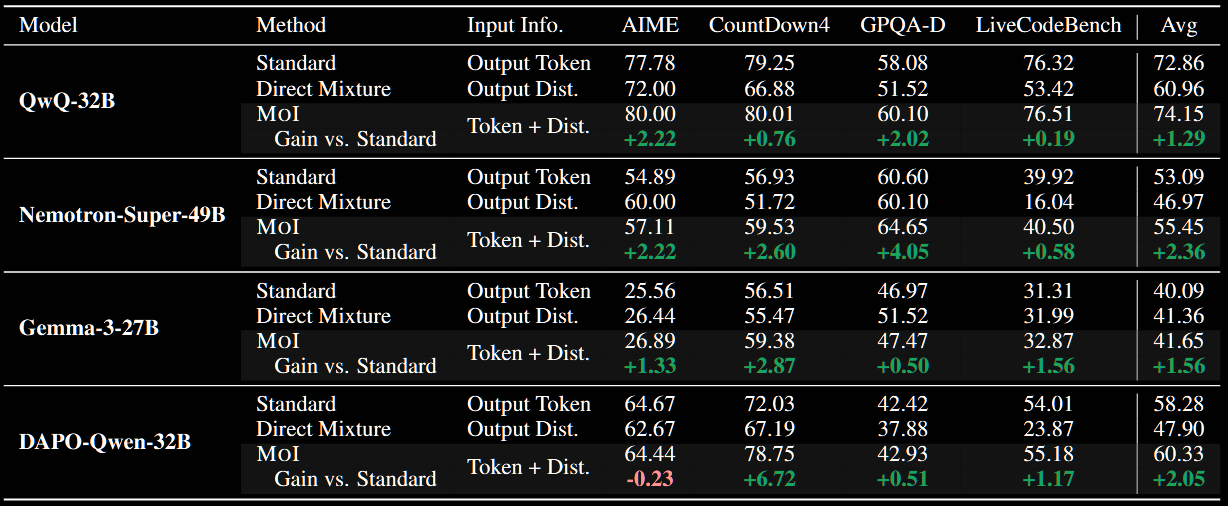
Comparison with Soft Thinking Paper

Interestingly, Direct Mixture frequently underperforms versus the baseline. This is somewhat in contradiction to the improvements seen in the Soft Thinking paper. The degradation is particularly pronounced for the Qwen models. The (model, benchmark) pair (QwQ-32B, GPQA-D) is used in both papers, but markedly different evaluations are reported in Soft Thinking.

• Soft Thinking paper:
  • CoT baseline → 64.17
  • CoT-Greedy → 65.15
  • Soft Thinking → 67.17
• Mixture of Inputs paper:
  • CoT baseline → 58.08
  • Direct Mixture → 60.10

The results for QwQ-32B on LiveCodeBench are significantly different too. One potential difference is the lack of a cold stop in Direct Mixture versus the Soft Thinking paper.