DeepSeekMath Summary

DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

• 2024-07; DeepSeek-AI

High-Level Summary

• Introduce DeepSeekMath 7B, a LLM focused on mathematical capabilities
• Achieves comparable performance with Minerva 540B, even with ~77x fewer parameters
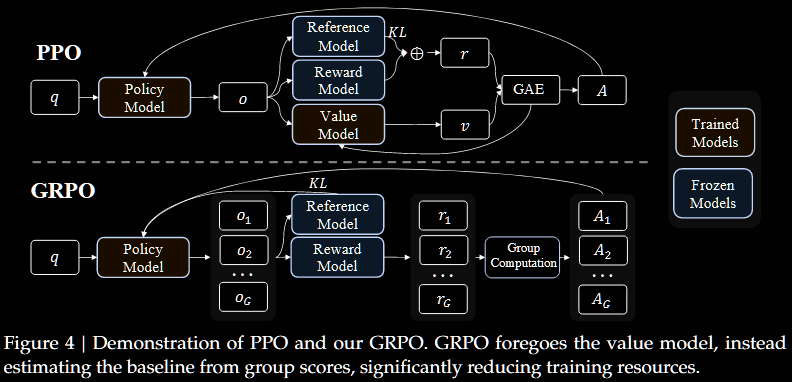
• Introduces and uses Group Relative Policy Optimisation (GRPO): GRPO foregoes the critic model, instead estimating the baseline from group scores
• Provide a unified paradigm to understand different models, and use to explore reasons behind the effective RL

The main theoretical contribution is the introduction of GRPO, which extends PPO.

Evolution: PPO to GRPO

Proximal Policy Optimisation (PPO) is an actor—critic RL algorithm which maximises a surrogate objective:

$$\theta_{k+1} = \arg\max_\theta \mathbb E_{q, a \sim \pi_{\theta_k}}[ J_\textsf{PPO}(q, o, \theta_k, \theta) ]$$

with

$$J_\textsf{PPO}(q, o, \theta', \theta) = \frac1{|o|} \sum_{t=1}^{|o|} \min\biggl\{ \frac{\pi_\theta(o_t \mid q, o_{< t})}{\pi_{\theta'}(o_t \mid q, o_{< t})} A_t, (1 + \textup{sgn}(A_t) \varepsilon) A_t \biggr\} - \beta D_\textsf{KL}( \pi_\theta \mathrel{\|} \pi_\textsf{rel}).$$

• $\pi_\theta$/$\pi_{\theta'}$ are the current/old policy models;
• $q$/$o$ are questions/outputs sampled from the question dataset/old policy;
• $A_t$ is the advantage based on the rewards and a learned value function;
• $\varepsilon$ is a clipping hyperparameter for stabilising training;
• $\beta$ is a hyperparameter governing per-token KL penalty.

The value function is treated as a baseline in estimating the advantage. In the LLM context, usually only the last token is assigned a reward score, which may complicate training a value function that is accurate at each token. Group Relative Policy Optimisation (GRPO) addresses this:

• it removes the need for additional value-function approximation;
• instead, it uses the average reward of multiple sampled outputs (to same question) as the baseline.

More specifically, for each question $q$, GRPO samples a group of outputs $\{o_1, ..., o_G\}$ from the old policy $\pi_{\theta'}$ and maximises an analogous surrogate objective

$$\textstyle J_\textsf{GRPO}(q, \{o_1, ..., o_G\}, \theta', \theta) = \frac1G \sum_{i=1}^G J_\textsf{PPO}(q, o_i, \theta', \theta).$$

except that now the advantage $A_t$ is replaced with the estimate $\hat A_{i, t}$ based on the rewards of the outputs inside each group only; in all its glory,

$$\textstyle J_\textsf{GRPO}(q, \{o_1, ..., o_G\}, \theta', \theta) = \frac1G \sum_{i=1}^G \frac1{|o_i|} \sum_{t=1}^{|o_t|} \min\bigl\{ \frac{\pi_\theta(o_{i, t} \mid q, o_{i, < t})}{\pi_{\theta'}(o_{i, t} \mid q, o_{i, < t})} \hat A_{i, t}, (1 + \textup{sgn}(\hat A_{i, t}) \varepsilon) \hat A_{i, t} \bigr\} - \beta D_\textsf{KL}(\pi_\theta \mathrel{\|} \pi_\textsf{rel}).$$

An unbiased estimator of $D_\textsf{KL}(\pi_\theta \mathrel{\|} \pi_\textsf{rel})$ is used, namely

$$D_\textsf{KL}(\pi_\theta \mathrel{\|} \pi_\textsf{rel}) \approx \frac{\pi_\textsf{ref}(o_{i, t} \mid q, i_{i, < t})}{\pi_\theta(o_{i,t} \mid q, o_{i, < t})} - \log \frac{\pi_\textsf{ref}(o_{i, t} \mid q, i_{i, < t})}{\pi_\theta(o_{i,t} \mid q, o_{i, < t})} - 1 \ge 0.$$

One of the key benefits of GRPO over PPO is not needing to learn/evaluate the advantage $A_t$, which can be costly. Two options are mentioned: "outcome" in #4.1.2 and "process" in #4.1.3. For example, in "outcome",

$$\hat A_{i,t} = \bigl( r_i - \textup{mean}(r) \bigr) / \textup{stddev}(r) \quad\text{for all}\quad t.$$

where $r_i$ is the reward for $o_i$ and $r = (r_i)_{i=1}^G$; in particular, the same advantage is prescribed to each timestep $\hat A_{i,t}$.

Key Differences: PPO vs GRPO

• Overview:

  • Traditional RL methods rely on external evaluators (critics) to guide learning

  • GRPO evaluates groups of responses relative to each other

  • This can lead to more efficient training, but requires multiple role-outs per example (the group of responses)

• Critic model (or lack thereof):

  • PPO requires a separate critic model to estimate the value, which often requires training

  • PPO's critic model typically comparable size to policy model, bringing substantial memory and computational burden

  • GRPO avoids this need, instead proposing a 'group' of outputs and calculates an advantaged based on the these rewards

  • GRPO adjusts the weights to direct output towards the better ones amongst the group

• Rough analogy:

  • If I perform a task once, I need a critic to say how well I do

  • If I perform it 10 times, I can compare the relative performances